On this page I give a popular introduction into my research focus on the
physics of strongly correlated electron systems and attempt to explain
why You should consider condensed matter physics fascinating.
Why is Condensed Matter Physics fascinating?
Condensed matter physics is the study of the structure and behavior of the matter that makes up most of the stuff that surrounds us every day. In addition to the field's tremendous technological successes, such as the discovery of transistor physics, NMR, superconducting electronics, etc., for most of us technology is neither our passion, nor do we need this crutch of applicational potential to fall back on. Indeed, sometimes the connection between our research and real world applications, or even materials is tenuous at best. This does not mean abstract research might never lead to the next pocket-jetpack, but rather that it is not focused towards an eventual application.

Electron map of the surface of manganese-doped gallium arsenide, on the brink of the metal-insulator transition. Adapted from Roushan/Yazdani Research Group.
The aspects of research that drives most of us is the awe and wonder we are privileged to experience these few moments when you figure out how something works, or more often the moments when find something you cannot explain. But more importantly: because it's fun.
Condensed matter physicists pursue novel states of matter at low temperature and study the emergence of collective phenomena. The field largely exists at the junction between statistical physics and quantum mechanics. We study large assemblies of electrons and nuclei in a condensed state, which often exhibit cooperative behavior and which is strikingly different from that of the individual constituents. It is amazing how many complex macroscopic phenomena originate from simple microscopic interactions. A single Zinc atom is not a metal, but thousands of Zinc atoms together are distinctly "metallic". Reduce the temperature to (close to) zero and the metal becomes superconducting. Or one carbon atom is not an insulator, but many of them together can be a diamond on your ring finger, or a sheet of graphene - the host of relativistic electrons. How does this work? That's part of what condensed matter physics is about.
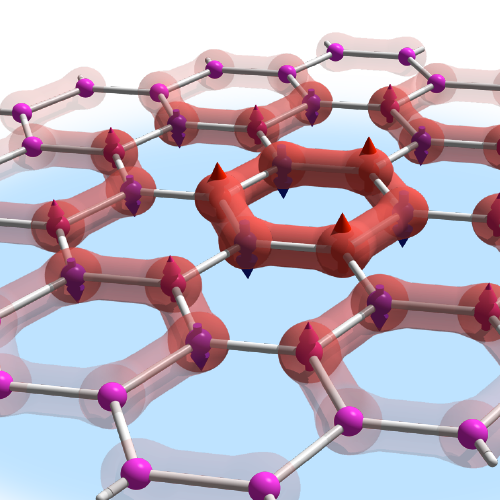
Illustration of a plaquette valence bond state - an electronic crystal at zero temperature which emerges from Dirac electrons with a simple onsite Coulomb repulsion.
Progress in the field is achieved by cooperative development coming from fresh theoretical ideas, from ideas transplanted to a novel context, and from experimental discoveries. In condensed matter physics, just as in any other field of physics, experiments play a key role. Some of these developments involve topics at the interface between condensed matter physics and other fields - examples include atomic physics, biology, economics, and particle physics. The diversity of condensed matter physics is a big part of the intellectual appeal of the subject.
Theoretical and computational condensed matter physics also include the study of models and states beyond the experimentally feasible at the very front of fundamental physics. The combination of quantum mechanics plus a large numbers of degrees of freedom has been proven to be a successful recipe for the emergence of exotic phenomena, especially when interactions between the particles become important.
Strong Correlations & the Universe in a Grain of Salt
The research topic of strongly correlated systems in condensed matter physics covers (mostly) crystalline materials and models, where two or more interactions are competing against each other at the same energy scale. Research in this area attempts to model and simulate existing materials, as well as to predict the properties of designed materials and models. This entails the challenge to understand the fundamental, complex interplay of many degrees of freedom, which can lead to exotic states of matter beyond the classical states we learn about in school (gas, liquid, sold, plasma).
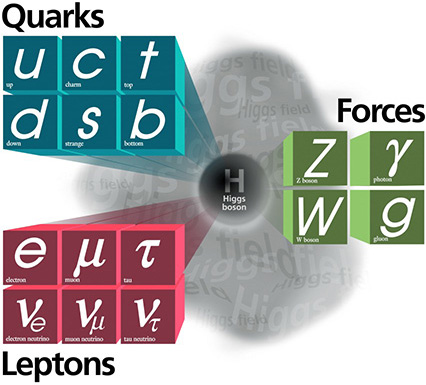
The Standard Model - a triumph of modern physics - allows us to explain all matter, from atoms to entire galaxies. Taken from here.
In contrast to high energy physics, which deals with the (possibly) fundamental particles of matter and forces in our current universe, in condensed matter hardly any degree of freedom we consider is fundamental, but the derived property of the underlying crystal, or model. Arguably, these very constrains are what make condensed matter physics even more sexy than particle physics. In contrast to particle physics which mostly deals with our universe as is (or was), condensed matter physicists build their very own and versatile universes, explore their own emerging forces and fundamental particles. In putting constraints on accessible energies and interacting degrees of freedom we can design independent micro-universes, which exhibit phenomena previously unseen. Both fields of research should be seen as complimentary topics in physics, which share remarkably similar methods, approaches and hence significant overlap.
The degrees of freedom we deal with in condensed matter physics are mostly (valence) electrons, phonons (from the atom cores and bound electrons) and their derived quasi-particles such as excitons, plasmons, polarons, skyrmions, spinons and others. Especially at low temperatures, where quantum effects dominate, strongly correlated systems can exhibit a multitude of phases, which have no classical analogues. Among them are high temperature superconductivity, heavy fermions, quantum spin liquids, topological insulators and many more.
Theoretical investigations of these systems are extremely challenging, since the importance of strong correlations causes most traditional methods to work only with very limited applicability, or fail altogether. Analytical approaches are constraint by approximations which are often difficult to control. Numerical techniques are often limited in the range of accessible system size and temperature.

Illustration of a strongly interacting ultracold gas in an optical lattice. Credit: Brad Baxley, JILA
My research combines aspects of statistical, computational and condensed matter physics, applying numerical approaches like
- Determinantal quantum Monte Carlo at zero and at finite temperature
- (Weak-coupling) continuous time quantum Monte Carlo
- Valence bond projector quantum Monte Carlo & stochastic series expansion
- Exact diagonalization
together with supporting analytical approaches. I put special emphasis on the use of methods without uncontrolled systematical errors, in order to allow for the best possible, unbiased answers to present-day problems in our field. My objective is to extend the accessible range of models and physics to study the interplay of different dynamical degrees of freedom. For specific topics covered in my research please see my list of publications.
